Euler’s Totient Function tells us about the number of integers, which are less than n and are co-prime to n.
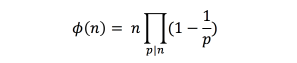
In other words, we can say that this function gives us the value of x for which x ≤ n and gcd(x, n) = 1.
Here, p is defined for the following conditions:
- p is a prime number
- n%p = 0, i.e., n is divisible by p.
- p ≤ n
Let us consider an example,
n = 10
The values of p would be 2 and 5, since 10%2 = 0 and 10%5 = 0, and 2 and 5 are prime numbers, less than or equal to 10.
Putting the above values in the Euler’s Totient Function, we get,
x = 10 x (1 – (1/2)) x (1 – (1/5))
x = 10 x (1/2) x (4/5)
x = 4
Verification:
There exist 4 numbers, {1, 3, 7, 9} which are less than or equal to 10, and are co-prime to 10.
There’s an another approach to this example, which is to iterate through all the numbers from 1 to n, and check for the gcd(i, n) at each iteration, and counting the numbers which gives a gcd of 1.
This would take O(n) time complexity to iterate through all the numbers from 1 to n, and an extra O(max(i, n)) to calculate gcd at each iteration.
An efficient approach is to pre-compute a sieve of prime numbers from 1 to n, and calculate the totient value by calculating the number of prime numbers in the sieve range.
Example:
Calculate the number of values of x for which
gcd(x, n) = g
Solution:
gcd(x, n) = g
Dividing both sides by g, we get
gcd(x/g, n/g) = 1
gcd(x’, n’) = 1, where (x’ = x/g and n’ = n/g)
Now, we can apply the totient function on this equation as Φ(n’) and find the answer.
In case, if n is not divisible by g, then, there doesn’t exist any value of x for which the equation gcd(x, n) = g holds true.
